LCS(Longest Common Sequence) 알고리즘
LCS
LCS(Longest Common Sequence)는 주어진 수열들에 대해 가장 긴 공통 부분 수열이다.
예를 들어, 두 문자열 BCDAACD와 ACDBAC에 대한 공통 부분 수열들은 다음과 같다.BC, CDAC, DAC, AAC, AC, CD ...
이러한 공통 부분 수열 중에서 가장 길이가 긴 부분 수열은 CDAC이다.
LCS는 $Dynamic Programming$을 이용해 접근할 수 있다.
알고리즘 동작
다음과 같은 두개의 수열 $X$,$Y$가 있다.


우선, $n = length(X), m = length(Y)$ 일 때, $(n+1)*(m+1)$크기의 dp배열이 필요하다.
그리고 다음과 같이 배열을 채운다.

dp[i][j]는 $X$의 i번째 원소와 $Y$의 j번째 원소까지 봤을 때, 현재까지 찾은 공통 부분 수열의 길이 중 가장 크기가 큰 값이다.
dp[i][j]는 다음과 같은 식으로 정의된다.
$dp[i][j] = 0 $ $ if (i=0 or j=0)$
$dp[i][j] = dp[i-1][j-1]+1 $ $ if (X[i-1] = Y[j-1])$
$dp[i][j] = MAX(dp[i-1][j],dp[i][j-1]) $ $ if (X[i-1] \neq Y[j-1])$
위 점화식을 이용해 차례대로 dp배열을 모두 채워 나아간다.

dp 배열을 모두 채웠을 때, dp[n][m]의 값이 주어진 두 수열의 LCS 길이다.
추적
LCS의 길이를 알았으니, 실제 LCS를 찾을 수 있다.
찾은 LCS의 길이를 $L$이라고 했을때, X[i-1]=Y[j-1]이고, dp[i][j] = $L$인 부분부터 역추적을 통해 LCS를 찾는다.
현재 위치(y,x)에서 X[y-1]=Y[x-1]이라면, stack에 $X[y-1]$ 또는 $Y[y-1]$를 push한다.
만약 X[y-1]$\neq$Y[x-1]라면, dp[y][x]가 채워졌던 방향으로 이동한다.
끝에 도달했을 때, stack에 있는 모든 원소를 pop하여 나열하면 하나의 LCS를 찾을 수 있다.
주어진 수열들에 대한 LCS는 여러개가 존재할 수 있음에 유의한다.

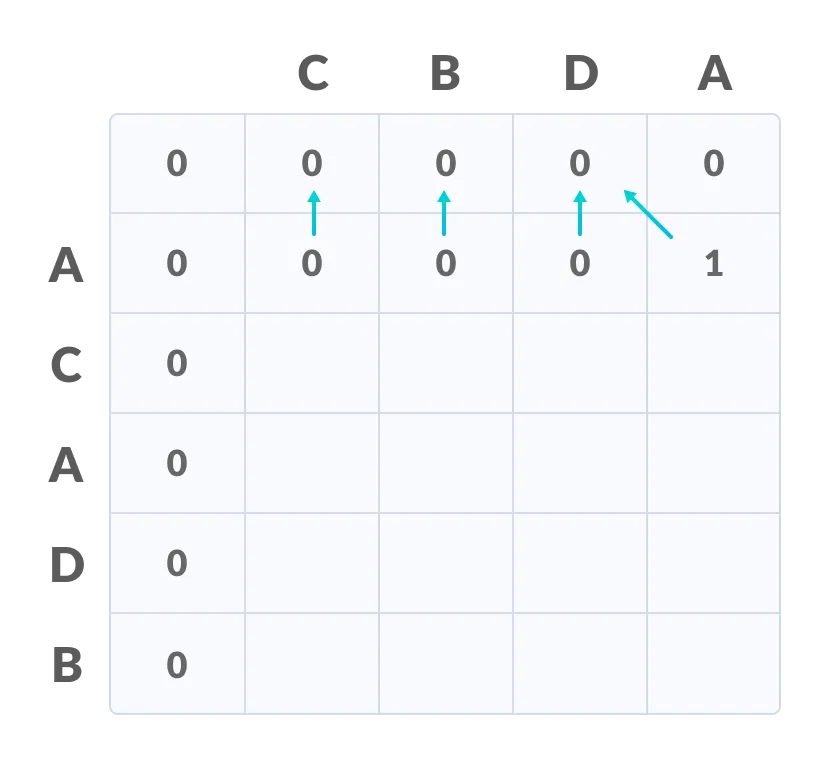
위 그림에서는 (3,4)지점부터 위 과정을 반복한 그림이다.
이를 통해 CA라는 하나의 LCS를 찾아낼 수 있다.
시간복잡도
두 수열 $X$, $Y$에 대해 $\theta(length(X)_length(Y))$의 시간복잡도를 가진다.
임의의 수의 수열에 대한 LCS는 NP-Hard의 복잡도를 가지는데, 수열의 개수가 $N$으로 일정하다면 다음과 같은 복잡도를 가진다.

출처 : https://www.programiz.com/dsa/longest-common-subsequence