펜윅트리(Fenwick Tree) 자료구조
펜윅트리(Fenwick Tree)
펜윅트리를 공부하기 전에 우선 세그먼트 트리에 대한 이해와 그 필요성에 대해 알아야한다.
세그먼트 트리는 구간의 정보를 빠르게 가져올때 사용한다.
기존 세그먼트 트리를 설명하면서 크기 N의 배열에 대해 필요한 트리의 사이즈는 2^(트리의 높이+1)이라고 잠시 짚고 넘어갔었다.
트리의 높이는 밑이 2인 logN이므로 트리를 구성하기 위해선 대충 4N정도의 크기가 필요하다.
또한 세그먼트 트리는 구현도 복잡하다..ㅎㅎ
펜윅트리은 이 문제를 해결할 수 있다. 결론부터 말하자면 크기 N의 배열에 대해 N만큼의 크기가 트리구성에 필요하고 구현또한 매우매우 간단하다. (이해만 한다면..)
펜윅트리를 이해하기 위해서는 또 한가지를 알아야 한다. 바로 비트마스크연산이다.
비트마스킹을 모른다면 구글에 검색하면 매우 좋은 설명들이 많다. (내 블로그엔 없다)
세그먼트 트리에 대한 이해, 비트마스킹에 대한 이해가 갖춰졌다면 펜윅트리를 구현할 수 있다.
설명
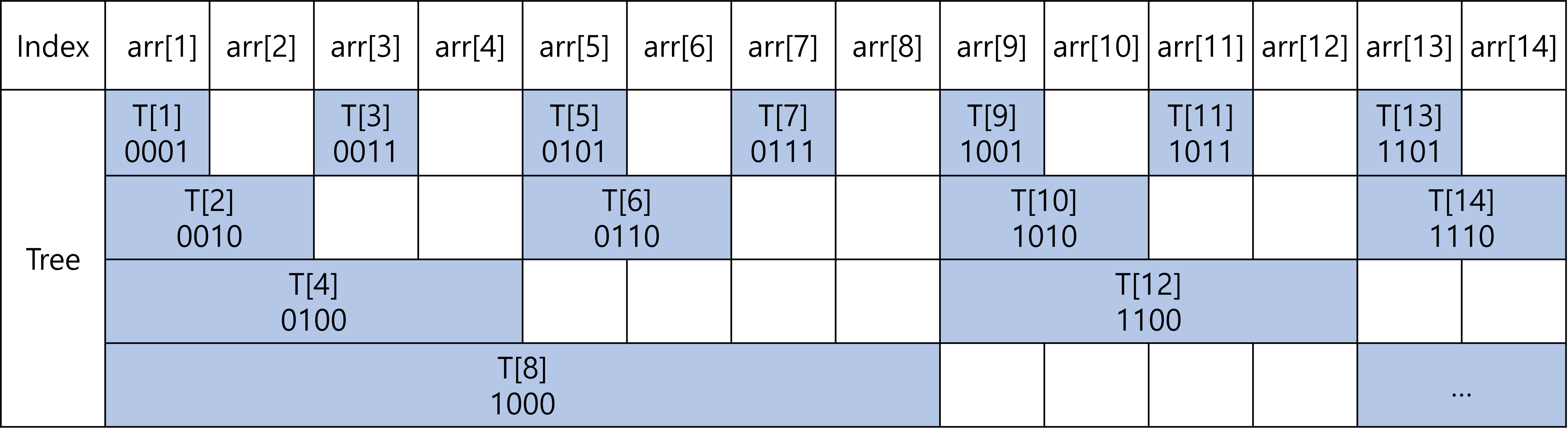
펜윅트리의 기본 구조는 다음과 같다.

다음과 같이 2의 배수와 짝수를 기준으로 구간의 합들이 저장된다. 위와 같이 구간의 합들을 저장하면 무엇이 좋을까?
구간트리의 두 요소인 업데이트와 구간정보 구하기를 기준으로 설명하자면,
업데이트의 관점에서, 만약 arr[10]의 값을 바꾼다면 arr[10]이 포함되어 있는 Tree배열의 값만 바꿔주면 된다.(T[10], T[12])
구간정보 가져오기의 관점에서, 만약 arr[13]까지의 합을 구하고 싶다면 T[13]+T[12]+T[8]을 통해 세번의 연산으로만 가져올 수 있다.
때문에 구간정보를 업데이트하고 가져오는데 O(logN)의 시간이 걸린다는 것을 짐작할 수 있다.
펜윅트리의 기본 구조에대해 이해했으니 구현단계로 넘어가야 한다. 이 과정에서 비트마스킹에 대한 이해가 필요하다.
구현
빠른 이해를 위해 위 표에서 트리의 인덱스를 2진수로 바꿔보았다.

이번에도 역시 원할한 설명을 위해 업데이트와 구간정보 가져오기 관점에서 설명을 한다.
또한 구간정보 업데이트의 기본인 구간합을 기준으로 설명한다.
1. 업데이트
- 예를 들어 arr[9]의 값을 바꾸려고 한다. 우리가 해야할 일은 arr[9]가 포함된 T[9], T[10], T[12]를 바꿔야 한다.
9,10,12를 이진수로 각각 바꿔서 나열해보면 다음과 같다.
1001 → 1010 → 1100
뭔가 규칙이 보인다! 바로 가장 오른쪽에 있는 1이 한칸씩 왼쪽으로 이동하는 것이다.
우연인지 아닌지 arr[3]로 다시 해보자. T[3], T[4], T[8]을 바꿔야 하므로
0011 → 0100 → 1000
0011에서 가장 오른쪽의 1이 왼쪽의 1과 합쳐지고 합쳐진 1은 왼쪽으로 이동할 수 있으므로 0100이 된다. 그리고 다시 가장 오른쪽의 1이 왼쪽으로 한칸 움직여서 1000이 되는것을 볼 수 있다.
위 규칙을 자세히 보면 가장 오른쪽에 존재하는 1만을 가지는 이진수와 더하는 것을 볼 수 있다.
말로 표현하니까 어려운데, arr[9]를 업데이트할때의 1001 → 1010 → 1100의 예시를 보자.
1001에서 비트의 값이 1인 가장 오른쪽 비트는 0001이다 1001+0001 = 1010이 되는것을 볼 수 있다.
다시 1010에서 비트의 값이 1인 가장 오른쪽 비트는 0010이다. 1010+0010 = 1100이 되는것을 볼 수 있다.
그렇다면 이렇게 1이 움직이는 연산을 어떻게 비트마스크로 표현할까?
비트의 값이 1인 가장 오른쪽의 비트만 찾으면 되므로 보수의 개념을 이용한다.
2의 보수에 대한 개념이 없다면 구글에서 공부를 하고 오자!
간단히 설명하자면 어떤 2진수에 대해 2의 보수란 1의 보수에 1을 더한것이다.
1의 보수란 모든 비트의 값을 반대로 바꾸는 것이다.(0은 1로, 1은 0으로)
예를 들어 10010의 1의 보수는 01101이고, 2의 보수는 1을 더한 01110이 된다.
신기하게도, 어떤 2진수와 그 2진수의 2의 보수를 AND하게 되면 가장 오른쪽 비트의 1만 나온다.
이는 비트연산에서 요긴하게 쓰이는 공식?이니까 알아두면 매우 편하다.
비트연산에 대한 설명이 길었다. 아무튼 arr[9]의 값을 바꾸면 T[9], T[10], T[12]의 값을 바꿔야 하는데
이때 1001 → 1010 → 1100로 진행하는 방법은 (자신의 수&자신의 2의 보수)를 더하면 된다는 것이다.
이를 코드로 나타내면 다음과 같다.
void update(int index, int diff) {
int idx = index;
while (idx <= n) {
tree[idx] += diff;
idx += idx & -idx;
}
}주의할 점은, 이미 tree배열에 기존의 값이 저장되어 있었으므로 기존에 있던 배열의 값과 새로 바꿀 값의 차이를 더해줘야 한다.
2. 구간정보 가져오기
구간의 정보를 가져올때도 위에서 사용한 비트마스크 연산을 사용한다.
arr[13]까지의 합을 구하고 싶다면 T[13]+T[12]+T[8]을 구하면 된다.
아까처럼 이를 2진수로 표현하면 다음과 같다.
1101 → 1100 → 1000
뭔가 또 규칙이 보이는 것 같다! 가장 오른쪽에 있는 1이 사라지고 있다.
위에서 가장 오른쪽에 존재하는 1을 가져오는 법은 (자신&자신의 2의 보수)라고 설명했기에, 이를 이용한다.
int sum(int index) {
int idx = index;
int result = 0;
while (idx > 0) {
result += tree[idx];
idx -= idx & -idx;
}
return result;
}어려운 아이디어에 비해서 정말 간단하게 구간의 정보를 가져올 수 있다.
똑똑한 사람들이라면 세그먼트 트리와 펜윅트리의 차이점을 바로 캐치했을 것이다.
가장 큰 차이점은 펜윅트리는 자료구조특성상 모든 구간합을 배열의 처음부터 구해야 한다. 세그먼트 트리처럼 특정구간의 합을 구하지 못한다.
예를 들어 세그먼트 트리는 arr[4]~arr[8]까지를 구할 수 있지만, 펜윅트리는 arr[1]~arr[8]의 구간합에서 arr[1]~arr[3]의 구간합을 빼야 한다.
때문에 구간의 합처럼 누적되는 값을 구할때는 펜윅트리를 사용할 수 있지만 최소값, 최대값 찾기 등 누적되지 않는 구간정보를 구할때는 펜윅트리를 사용할 수 없다.
구간의 곱도 펜윅트리를 통해 풀려고 했는데 매우매우 복잡하고 어려워서 그냥 세그먼트 트리로 풀었다.
또한 세그먼트 트리와 다르게 펜윅트리에서의 배열은 1부터 시작해야 한다. 비트연산을 해야하기 때문에 0은 사용할 수 없다.