세그먼트 트리(Segment Tree) 자료구조
세그먼트 트리(Segment Tree)
구간의 정보를 업데이트하고 가져올때는 어떤 방법을 사용할까?
가장 쉽게 생각나는 방법은 업데이트시 해당 배열의 값을 바꾸고, 다시 가져오는 방법이다.
예를 들어 arr[4] = {1,2,3,4}라는 배열이 있고, 다음의 작업을 수행한다고 가정하자.
1. arr[0]~arr[3]까지의 합을 구한다.
2. arr[3]의 값을 5로 변경한다.
3. arr[0]~arr[3]까지의 합을 구한다.
해당 내용을 위에서 언급한 방식대로 진행하면 인덱스 0~3까지의 배열의 합을 구하고 (Θ(N)) arr[3]의 내용을 바꾼뒤 다시 0~3까지의 배열의 합을 구해야 한다(Θ(N)).
위의 예시는 배열의 크기가 작기때문에 위의 방식대로 해도 큰 문제가 없지만, 배열의 크기가 매우 커지고, 연산을 하는 수도 매우 많아지면 그땐 문제가 발생한다.
세그먼트 트리는 이 구간의 정보를 업데이트하고 가져오는 방식을 빠르게할 수 있다.
세그먼트 트리
설명
- 세그먼트 트리는 정보를 업데이트 하고 빠르게 구간의 정보를 가져오고 싶을 때 사용하는 자료구조다.
- 기본 이진트리로 구성되었으며 크기 N의 배열에 대해서 세그먼트 트리를 구성하고 싶을 경우 세그먼트 트리 배열의 크기는 2^(트리의 높이+1)이다.
트리의 높이는 좀만 생각하면 바로 구할 수 있다
그림을 보면서 이해하는 것이 빠르다.
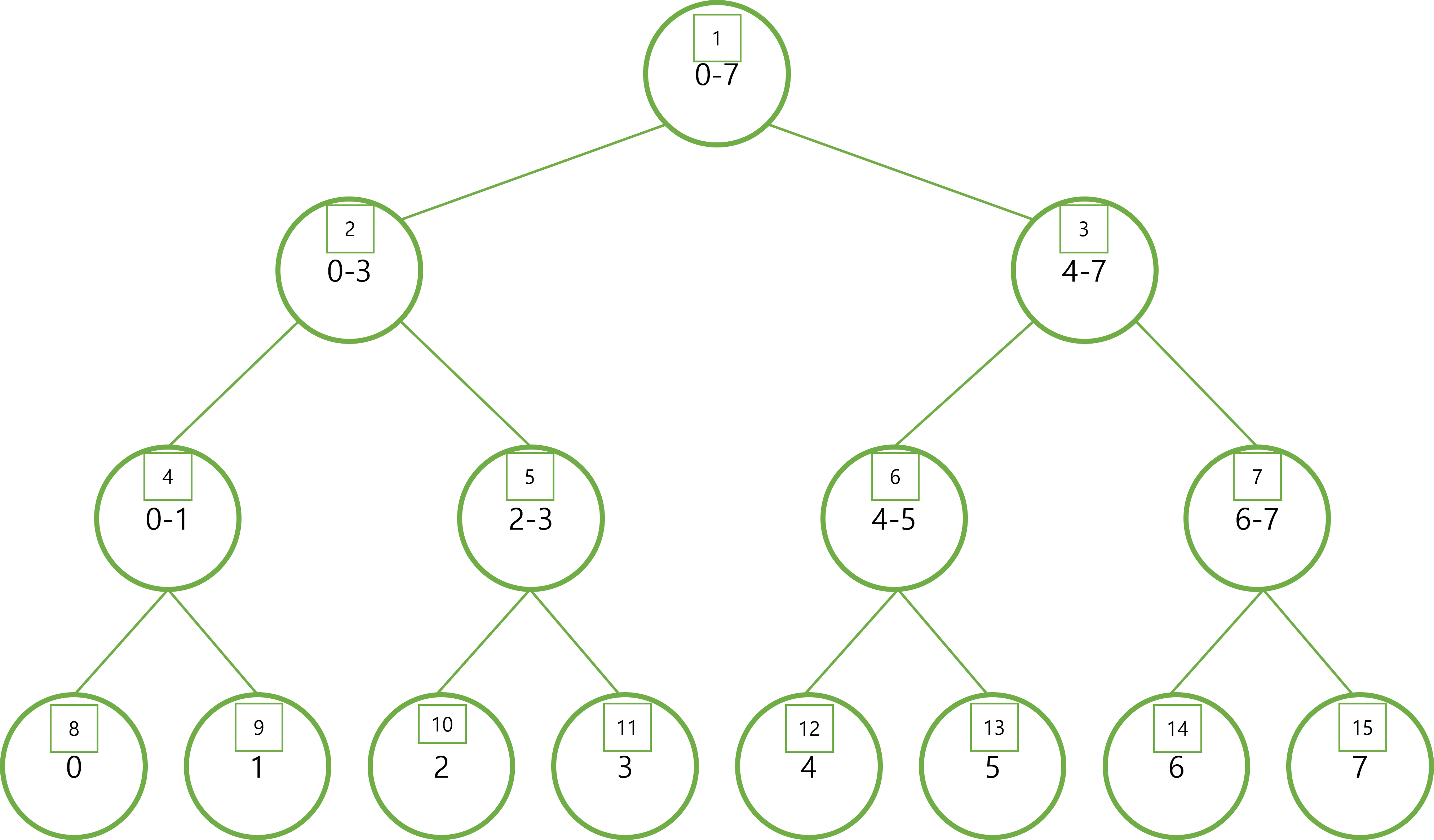
각 노드의 네모칸 안에있는 번호가 노드의 번호이다.
N이 8이라고 가정한다. 각 리프노드 (8~15)는 배열의 값(arr[0]~arr[7])을 저장하고 있다.
나머지 노드들은 하위 노드들에 대한 구간의 정보를 가지고 있다. 예를 들어 3번 노드는 arr[4]~arr[7]까지의 정보를 담고 있는 것이다.
세그먼트 트리의 사용이유는 위에서 언급했듯이 구간의 정보를 업데이트하고 빠르게 가져오는 것이다.
아래 예시를 보며 따라가보자. 세그먼트 트리의 가장 기본인 구간합에 대해서 진행해 볼것이다.
arr[8] = {0,1,2,3,4,5,6,7,8}이라는 배열이 있다. 이 배열을 트리에 업데이트 시키면 다음과 같다.
빨간숫자는 구간의 합을 나타내고 있다.

위 그림에서 arr[4]의 값을 8로 바꾸면 트리의 값이 다음과 같이 변화한다.
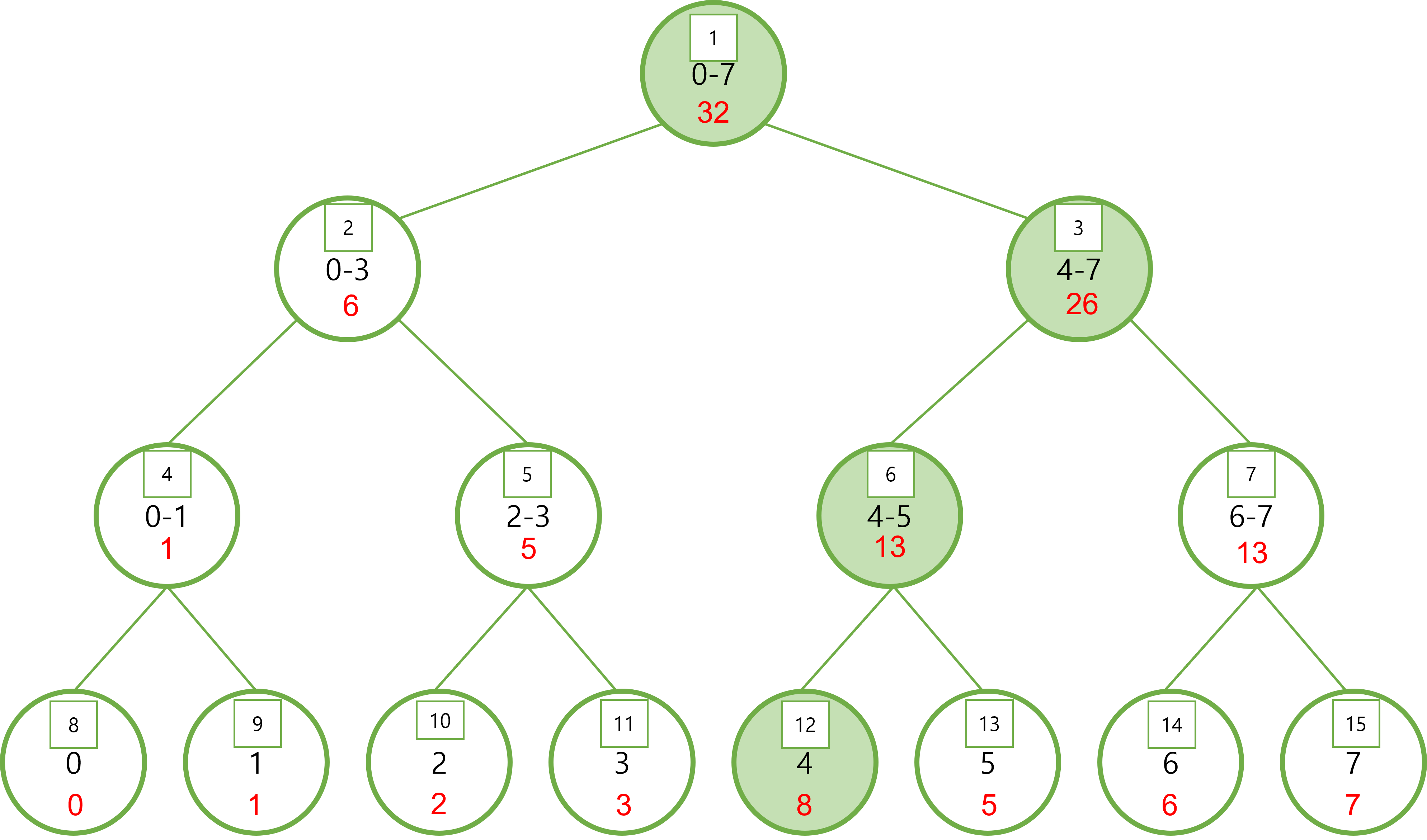
색칠한 노드들이 바뀐 부분이다.
왜 구간합에서 세그먼트 트리를 사용해야 하는지 감이 오는가?
세그먼트 트리를 사용하지 않고 배열의 값을 바꾸고 구간의 합을 다시 가져올때는 다음과 같은 시간이 걸린다.
O(1) (업데이트) + O(N) (구간합 구하기) = O(N)
하지만 세그먼트 트리을 사용하면 걸리는 시간은 다음과 같다.
O(logN) (업데이트) + O(1) (구간합 가져오기) = O(logN)
즉, 세그먼트 트리의 시간복잡도는 O(logN)이다.
구현
그렇다면 구현은 어떻게 할까?
세그먼트 트리의 가장 기본인 구간합을 기준으로 설명한다.
세그먼트 트리를 구성하고 구간의 정보를 가져오기 위한 많은 코드들이 있지만 다음 두개의 함수면 모두 구현가능하다.
1. 업데이트
2. 구간정보 가져오기
1. 업데이트
이해를 돕기위해 초기 트리를 다시 가져왔다.
이진트리를 공부해본 사람이라면 알겠지만 상위노드에서 두개의 하위노드를 선택하는 방식은 2*index (왼쪽 자식노드)와 2*index+1 (오른쪽 자식노드)이다. 예를 들어 7번노드의 두 자식은 14(7*2)번 노드와 15(7*2+1)번 노드이다.
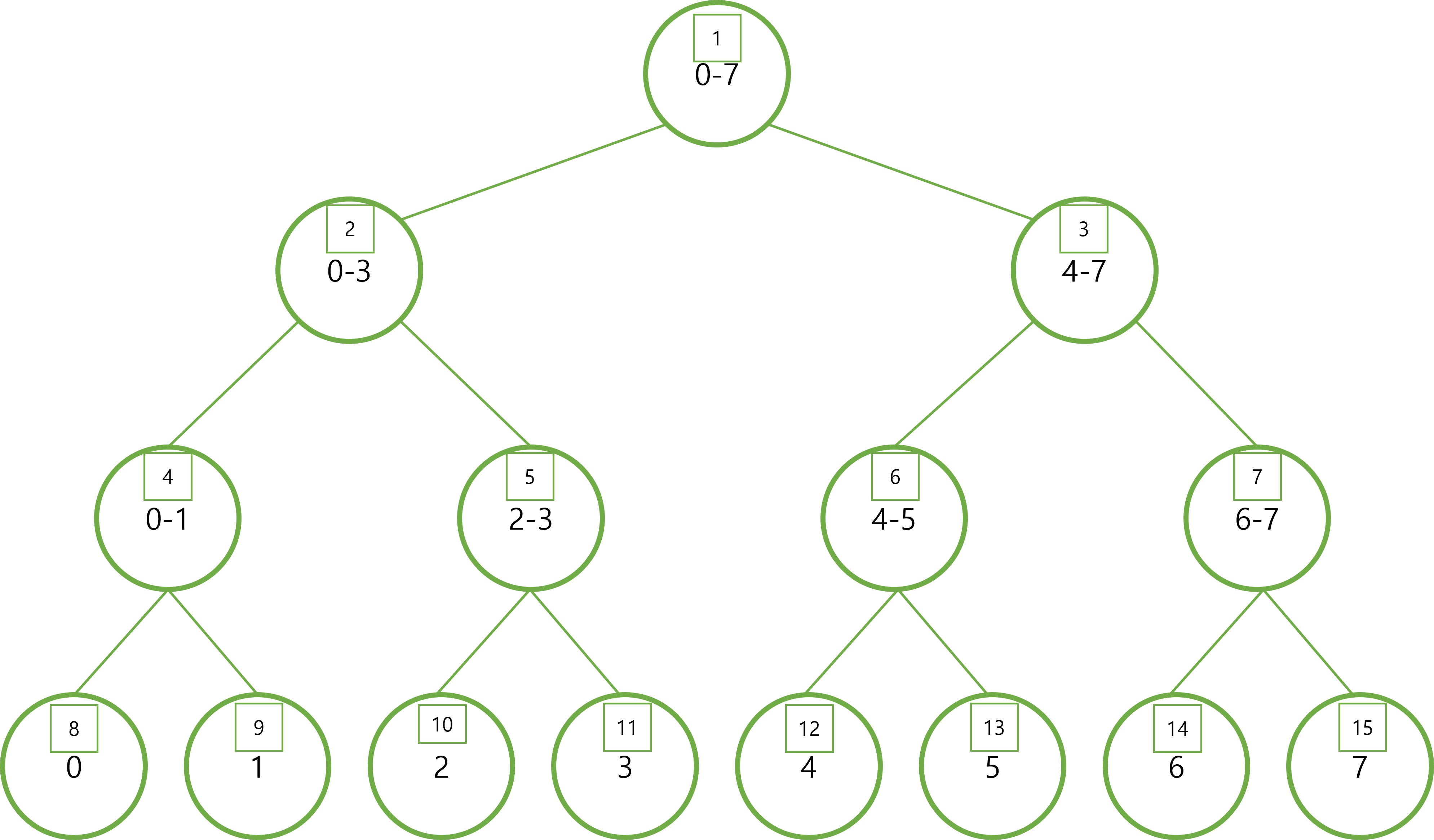
업데이트는 루트노드부터 구간을 좁혀가며 재귀의 형식으로 진행된다. 초기 값은 바꿀 배열의 인덱스(K)와 바꿀값(V), 그리고 배열의 시작부터 끝(0~7)으로 설정한다. 그리고 반으로 쪼개며 하위노드로 내려가는 방식이다.
- 쪼개진 구간의 범위가 K를 벗어나면 해당 노드의 값을 리턴한다.
- 상위 노드에 두 하위 노드의 합을 저장한후, 리턴한다.
- 계속 반복하다보면 시작과 끝이 같아지는 지점에 도착한다. 그 노드가 바로 리프노드이다. 이때 노드에 V을 저장한 후, 리턴한다.
함수가 호출됐던 곳으로 계속 리턴하며 세그먼트 트리는 최종 업데이트까지 마치게 된다.
코드를 천천히 따라가보면 이해가 된다!
int update(int node, int K, int V, int start, int end){
if(K<start || end<K) return tree[node] ;
if(start==end) return tree[node] = V;
int mid = (start+end)/2;
return tree[node] = update(node*2, K, V, start,mid) + update(node*2+1, K, V, mid+1, end);
}2. 구간정보 가져오기
구간의 정보가져오는 것 역시 위에서 했던 방법과 비슷하다.
루트노드부터 시작하여 구간을 좁혀가며 재귀의 형식으로 진행된다. 초기값은 배열의 시작과 끝(start ~ end)과 알고 싶은 구간의 시작과 끝(left~right)이다.
위의 방식과 마찬가지로 start와 end를 좁혀나가며 세가지 경우의 수에 따라 다르게 진행된다.
1. start~end 구간이 left~right구간에 속하지 않는 경우
- 리턴이 되어도 결과에 영향을 주지 않는 값을 리턴한다. (예를 들어 구간합이면 0, 구간곱이면 1 등)
2. start~end 구간이 left~right구간에 속하는 경우
- 해당 노드의 값을 리턴한다.
3. start~end 구간이 left~right구간에 걸치는 경우
- 구간을 반으로 쪼개 재귀를 하고 두 하위노드의 합을 리턴한다.
코드를 천천히 따라가보면 이해가 된다!
int sum(int node, int start, int end, int left, int right){
if(end<left || start>right) return 0;
if(start>=left && end<=right) return tree[node];
int mid = (start+end)/2;
return sum(node*2, start,mid,left,right)+sum(node*2+1,mid+1,end,left,right);
}
복잡한 아이디어에 비해 코드구현은 비교적 간단해보인다.
이것만 그대로 가져다 써도 무려 백준에서 골드1티어 문제인 2042(구간합 구하기)를 해결할 수 있다!