C++ 백준 2270 (하노이 탑)
백준 2270 (하노이 탑)
https://www.acmicpc.net/problem/2270
2270번: 하노이 탑
첫째 줄에 정수 n(1≤n≤100,000)이 주어진다. 둘째 줄에는 세 정수 a, b, c가 주어진다. 이는 차례로 1, 2, 3번 막대기에 꽂혀 있는 디스크의 개수이다. 이는 0이상 n이하이며, a+b+c=n이다. 다음 3개의 줄
www.acmicpc.net
기본 하노이탑 문제 응용버전이다.
하노이탑 기본문제 (1~N까지 차례로 쌓인 탑을 다른 rod로 옮기는 문제)는 여기(링크)에 있다. 꼭 이해하고 오자.
1~N까지의 차례로 쌓인 탑을 옮길때는 2^N-1만큼의 횟수가 소요된다고 했다.
그렇다면 탑이 차례로 쌓여있지 않고 뒤죽박죽 섞여있을 때는 어떻게 될까?
이 문제가 바로 그것이다.
문제에서는 어디로 하노이탑을 쌓아야 하는지도 묻고있는데 이는 쉽다.
가장 큰 원판이 있는곳으로 모으면 된다. (걸리는 횟수가 2^(원판의 크기)이기 때문에 가장 큰 원판이 있는 곳으로 모은다면 2^(가장 큰 원판의 크기)만큼의 횟수가 필요없기 때문) <- 이해가 안된다면 기본 하노이탑 문제(링크)를 꼭꼭 다시 봐야한다!!
설명
기본적인 아이디어는 거꾸로 하는 것이다.
어떤 과정이었든 하노이탑은 원하는 rod에 쌓여질 수 있다.
즉 원하는대로 쌓여진 하노이탑에서 거꾸로 재귀를 호출하며 처음 주어진 상태를 완성시키는 방식으로 하면 된다.
말로 백번 설명해봤자 이해못한다. 그림을 보며 이해해보자.
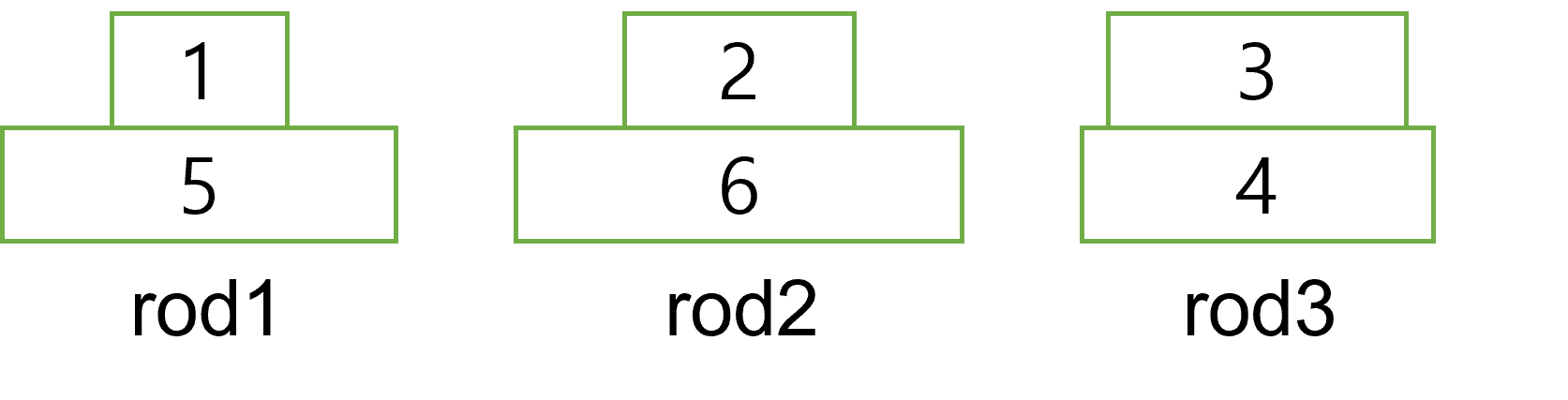
다음과 같이 뒤죽박죽 섞인 탑들이 있다고 하자.
만약 내가 탑을 쌓기 원하는 rod가 3번 rod라고 한다면 최종 모양은 다음과 같다.

위 모양이 나오기 위해 전단계에서는 다음과 같은 모양이 나왔어야 했다. (밑이 6인과정)

이때, 6번원판을 rod3으로 옮기는 과정(1)과 1~5번 원판을 rod3으로 옮기는 과정(2^5-1)이 더해져 총 횟수는 2^5이 된다.
이때 5번원판은 이미 rod1에 존재하기 때문에 밑이 5인과정은 할 필요가 없다.
그리고 또 이 단계가 나오기 위해 전단계에서는 다음과같은 모양이 나왔어야 했다. (밑이 4인과정)
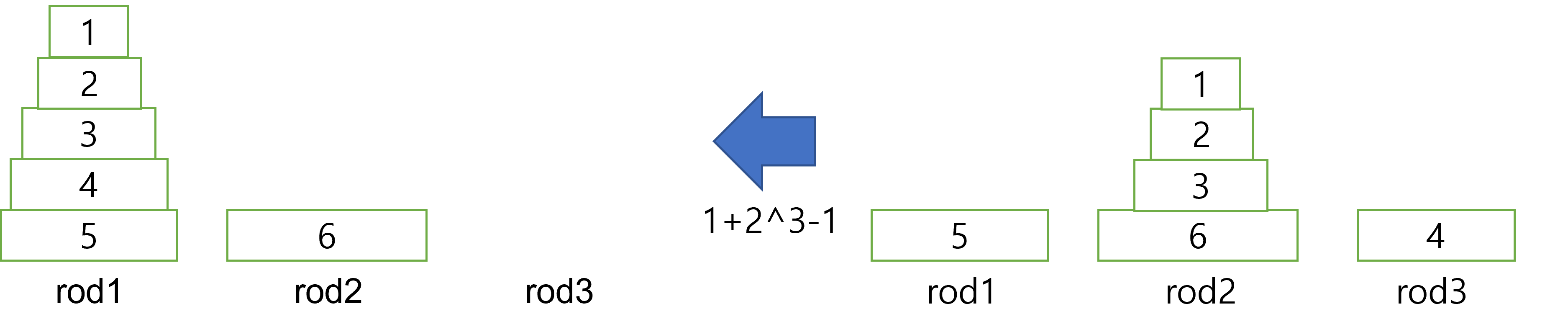
4번원판을 rod1으로 옮기는 과정(1)과 1~3번 원판을 rod1으로 옮기는 과정(2^3-1)이 더해져 총 횟수는 2^3이 된다.
계속 과정을 진행해보면 다음과 같다.



이로써 처음모양이 나왔다. 지금까지의 과정에서 더해졌던 횟수를 더하면 32+8+4+2+1 = 47이므로 답은 47이다.
또, 처음에서 말했듯이 가장최소횟수가 되려면 가장 큰 원판이 있는 곳으로 탑을 쌓으면 되기때문에 문제를 쉽게 해결할 수 있다.
구현
#include <iostream>
using namespace std;
int pow[1000001];
int rod[1000001];
int a,b,n,k;
long long ans=0;
void make_pow(int n){
pow[0]=1;
for(int i=1;i<=n;i++){
pow[i]=(2*pow[i-1]%1000000);
}
}
void go(int size, int dst_rod){
if(size<=0) return;
if(dst_rod==rod[size]){
go(size-1, dst_rod);
return;
}
int tmp_rod = -(dst_rod+rod[size]);
ans+=pow[size-1];
ans%=1000000;
go(size-1, tmp_rod);
}
int main(){
ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
cin>>n;
int num_rod[3];
for(int i=0;i<3;i++){
cin>>a;
num_rod[i]=a;
}
make_pow(n);
for(int i=-1;i<=1;i++){
for(int j=0;j<num_rod[i+1];j++){
cin>>b;
rod[b]=i;
if(b==n) k=i;
}
}
go(n,k);
cout<<k+2<<"\n";
cout<<ans;
return 0;
}구현을 쉽게하기 위해 rod를 -1, 0, 1로 구현했고 답을 출력할때만 2를 더해줬다.
무려 골드 2티어 문제를 이해하고 풀었다.