C++ 백준 1948 (임계경로)
백준 1948 (임계경로)
https://www.acmicpc.net/problem/1948
1948번: 임계경로
첫째 줄에 도시의 개수 n(1 ≤ n ≤ 10,000)이 주어지고 둘째 줄에는 도로의 개수 m(1 ≤ m ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 도로의 정보가 주어진다. 처음에는 도로의
www.acmicpc.net
설명
이 문제는 임계경로의 길이와 그 경로들에 채택되었던 간선의 개수를 세는 문제이다.
임계경로의 길이를 구하는 방법은 여기(링크)에 있다.
임계경로는 하나만 존재하는 것이 아니라 여러개 존재할 수도있다. 때문에 이 임계경로들에 채택되었던 간선의 개수를 세는 방법은 꽤 어려웠다.
여러 방법을 통해 임계경로들에 채택되었던 간선의 개수를 셀 수 있다.
그러나 이 글에선 내가 생각하기에 가장 쉬웠던 방법을 설명하겠다.
(아마 인터넷에 있는 여러 방법 중 이 방법이 젤 쉬울거임)
기본적인 아이디어는 다음과 같다. 문제의 시작지점 start, 끝지점 end
A. 임계경로 길이찾기 알고리즘을 통해 각 지점마다 시작지점으로부터 최장경로의 길이를 저장
B. A에서 찾은 임계경로들에 채택되었던 간선의 개수를 셈.
A.
1. start부터 end까지 임계경로의 길이를 찾는 알고리즘을 통해 각 지점마다 start로부터 가장 길었던 경로의 길이를 저장한다. = org_dis[해당노드]
2. 그래프를 reverse시킨 뒤 end부터 start까지 위 과정을 반복한 후 각 지점마다 end로부터 가장 길었던 경로의 길이를 저장한다. = rev_dis[해당노드] (그냥 1번과정을 그래프를 뒤집은 후 다시 한 후 다른 배열에 저장하는 거다.)
다음 B는 정방향 그래프로 해도 되고 뒤집은 그래프로 해도되는데 쉽게 정방향 그래프로 하겠다.
B.
1. start부터 bfs로 노드를 탐색한다.
2. bfs를 돌며 다음 두가지 조건을 만족해야 한다.
- 2-1) org_dis[현재노드]+다음노드까지 거리 = org_dis[다음노드]
- 2-2) org_dis[다음노드]+rev_dis[다음노드]=A에서 찾은 임계경로의 길이
위 조건을 모두 만족하면 다음노드를 queue에 push하고 전체카운트(찾은 간선의 개수)를 하나 더한다.
정방향 그래프로 bfs를 했을 때와 역방향 그래프로 bfs를 했을때 서로 시작과 끝에서 해당노드까지의 거리의 합이 임계경로의 길이와 같다면 해당 간선은 채택된 것이다.
다음과 같은 그래프가 있다.
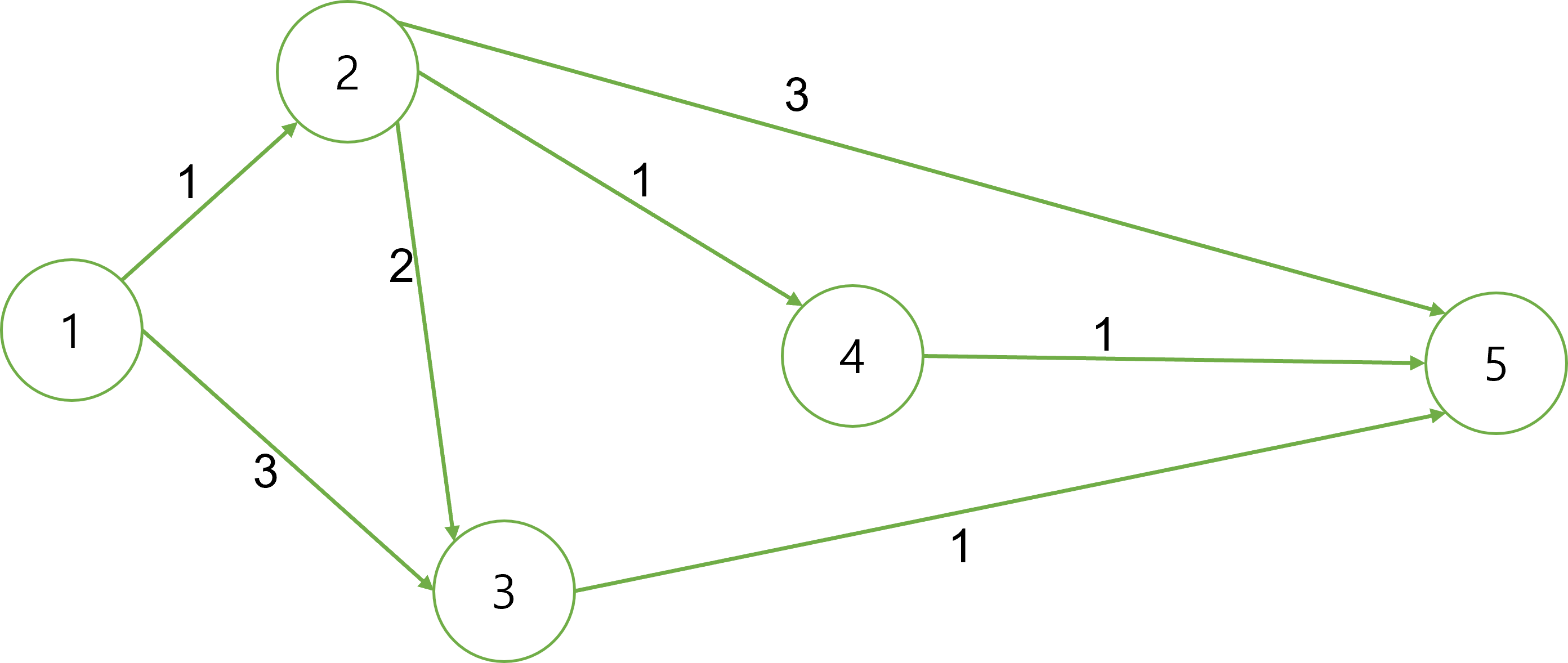
위 그래프를 1에서 5까지의 임계경로를 구하고 각 정점의 최장거리는 org_dis(빨간색)
위 그래프의 역방향그래프를 5에서 1까지 임계경로를 구하고 각 정점의 최장거리 는 rev_dis (파란색)

여기까지가 A번을 완료한 모습이다.
그러면 이 문제의 핵심 임계경로들의 간선을 찾아야 한다.
역방향 그래프로 해도되고 정방향 그래프로 해도되지만 편의상 정방향 그래프로 BFS(시작:1, 끝:5)를 진행한다.
노란간선은 현재 BFS로 체크중인 간선임을 뜻하고 빨간간선은 조건을 모두 만족하여 채택된 간선이다.
위 B단계에 대한 설명을 잘 생각해보며 따라가보자. (2-1)과 (2-2)두가지 조건을 모두 만족해야함

이로써 총 3개의 간선이 채택되었음을 알 수 있다.
주의할 점은 이미 방문했던 노드는 다시 방문하면 안된다.
구현
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
int n,m;
int ans=0;
int res_dis;
void bfs(vector <vector <pair<int ,int>>> &graph, int start, int *dis, int *indeg){
bool visit[100001];
for(int i=1;i<=n;i++){
visit[i]=false;
}
queue <int> q;
q.push(start);
while(!q.empty()){
int curr = q.front();
q.pop();
if(visit[curr] || indeg[curr]!=0) continue;
visit[curr]=true;
for(int i=0;i<graph[curr].size();i++){
int des = graph[curr][i].first;
if(dis[des]<dis[curr]+graph[curr][i].second) {
dis[des] = dis[curr]+graph[curr][i].second;
}
q.push(des);
indeg[des]--;
}
}
}
void find_count(int start, int end, vector <vector <pair<int ,int>>> &graph, int *org_dis, int *rev_dis){
bool visit[100001];
for(int i=1;i<=n;i++){
visit[i]=false;
}
queue <int> q;
q.push(start);
visit[start]=true;
while(!q.empty()){
int curr = q.front();
q.pop();
for(int i=0;i<graph[curr].size();i++){
int des = graph[curr][i].first;
int weight = graph[curr][i].second;
if(weight+org_dis[curr]==org_dis[des] && org_dis[des]+rev_dis[des]==res_dis) {
if(!visit[des]){
visit[des]=true;
q.push(des);
}
ans++;
}
}
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);\
cin>>n>>m;
int start, end;
vector <vector <pair<int ,int>>> org_graph(n+1);
vector <vector <pair<int ,int>>> rev_graph(n+1);
int a,b,c;
int org_dis[100001];
int rev_dis[100001];
int org_indeg[100001];
int rev_indeg[100001];
for(int i=1;i<=n;i++){
org_indeg[i]=org_dis[i]=0;
rev_indeg[i]=rev_dis[i]=0;
}
for(int i=0;i<m;i++){
cin>>a>>b>>c;
org_graph[a].push_back({b,c});
rev_graph[b].push_back({a,c});
org_indeg[b]++;
rev_indeg[a]++;
}
cin>>start>>end;
bfs(org_graph, start,org_dis, org_indeg);
bfs(rev_graph, end,rev_dis, rev_indeg);
res_dis = org_dis[end];
find_count(start, end, org_graph, org_dis, rev_dis);
cout<<res_dis<<"\n"<<ans;
return 0;
}
임계경로의 길이만 찾는 것은 매우 간단하게 해결할 수 있었지만 채택된 간선을 찾는 일은 난이도가 있었다.
지나왔던 경로를 출력하려면 DFS를 통해 모두 반복해보면 되지만, 간선을 찾는 것은 중복이 되면 안되기 때문이다.
이 글을 이해했다면 무려 플래티넘5단계의 문제를 완벽히 이해하고 풀은것이다!