DFS
BFS와 같이 탐색에 이용되는 대표적인 알고리즘이다.
BFS(Breadth-First Search)
설명 탐색을 위해 사용되는 알고리즘이다. 이름에서 알 수 있듯이, 너비를 우선으로 탐색하기 때문에 단계적인 탐색을 위해 사용된다. 여기서 탐색이란, 대표적으로 그래프에서 정점 방문을 예
seongmok.com
너비를 우선으로 단계적으로 탐색했던 BFS와 달리 DFS는 깊이를 우선으로 탐색하기 때문에 방문하지 않은 이웃 단계를 최대한 깊게 탐색할 수 있는 만큼 하는 것을 목적으로 한다.
예제를 보며 이해해보자.
다음과 같은 그래프가 있다. 정점1에서 출발하여 모든 정점을 탐색하는데, 이때 위 목적을 바탕으로 움직일 것이다.
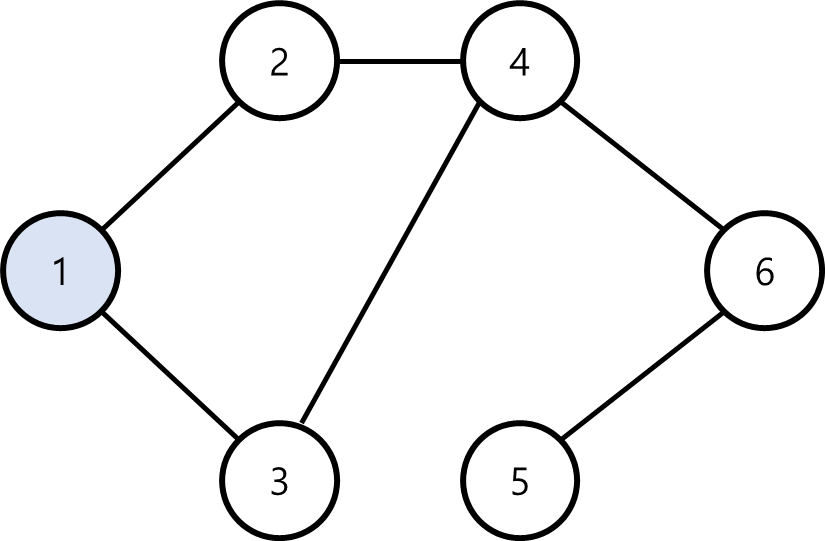
불필요한 중복 방문을 막기 위해 현재 정점을 방문체크 한 뒤, 이웃한 정점 중 방문하지 않은 정점으로 이동한다.
이때, 이웃한 정점중 어느 정점을 우선으로 탐색할 것인지에 대한 우선순위를 정할 수도 있다.
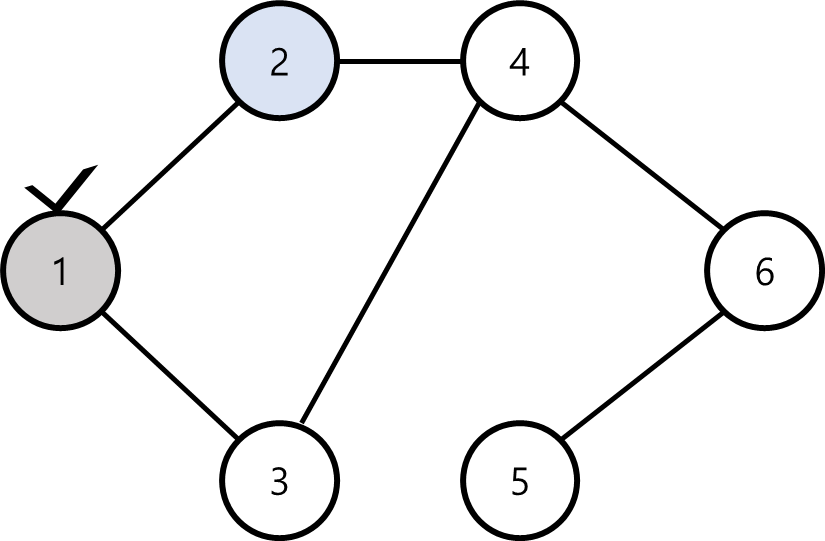
이 과정을 계속 반복하면 다음과 같은 과정을 거치게 된다.

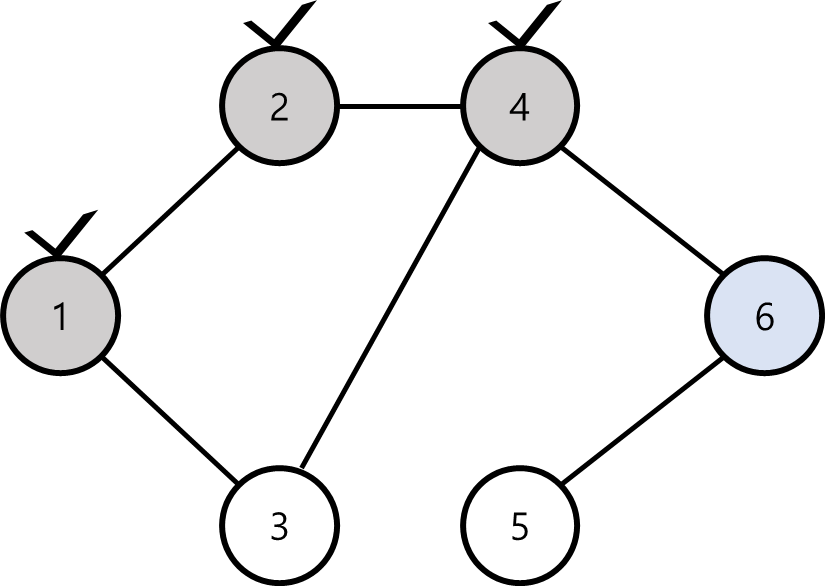
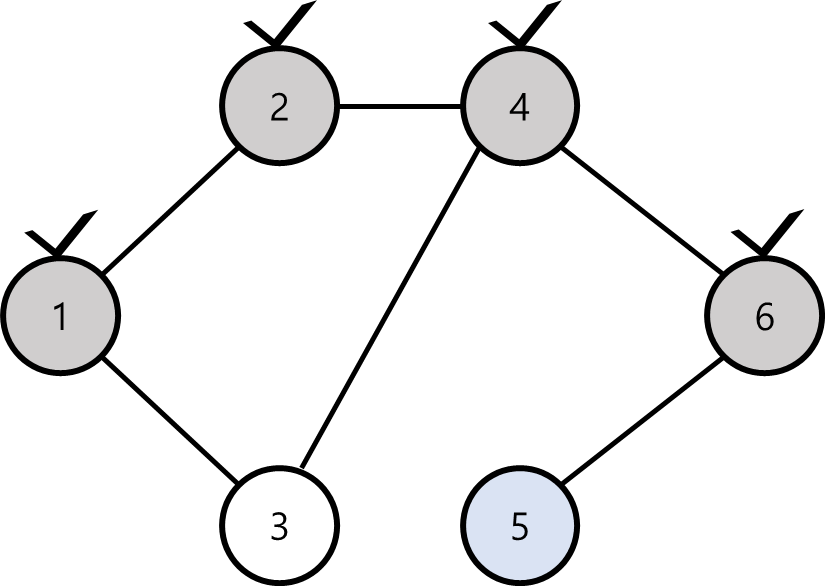
현재 정점5까지 왔는데, 이제 더이상 방문하지 않은 이웃 정점이 존재하지 않는다.
그러므로 왔던 길을 통해 방문하지 않은 이웃 정점이 존재했던 정점으로 다시 되돌아가야 한다.
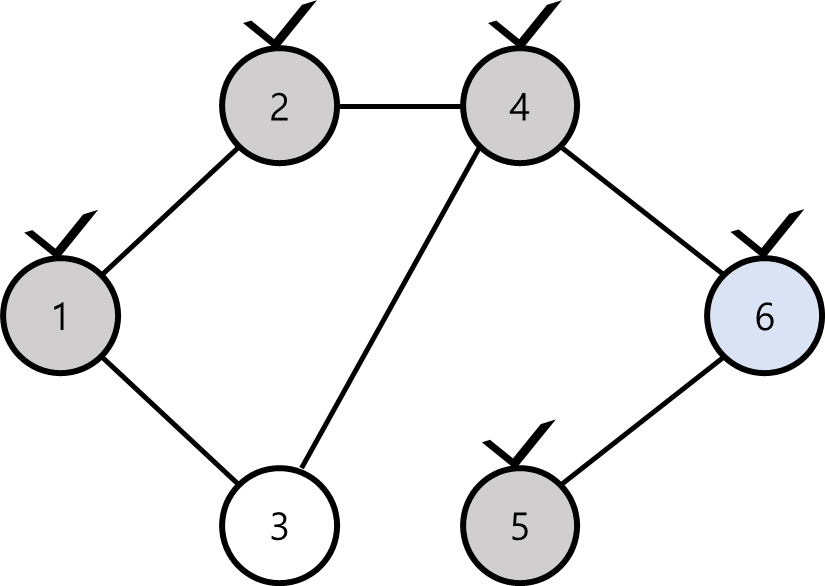
바로 이전 정점인 정점6으로 되돌아왔다.
하지만 역시 방문하지 않은 이웃 정점이 존재하지 않으므로 다시 되돌아간다.

정점4에서는 방문하지 않은 이웃 정점이 존재하므로 과정을 진행할 수 있다.

또한 다시 정점3에서 더 이상 진행할 수 없으므로 왔던 길을 통해 되돌아간다.
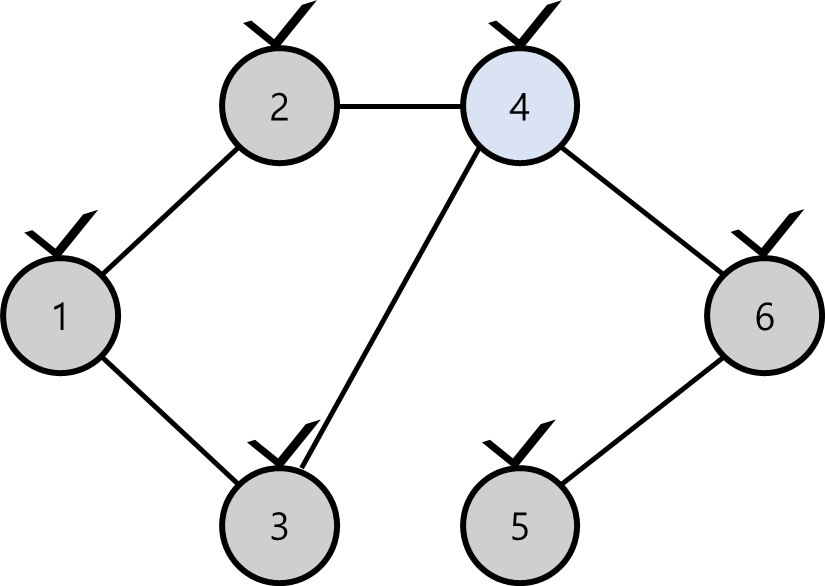


시작 정점인 정점1로 다시 되돌아 왔으므로 DFS 과정을 마친다.
이로써 모든 정점을 깊이순으로 방문할 수 있다.
그래프에서의 정점방문 뿐만 아니라 여러 상황에서 응용할 수 있다.
또한 이후의 과정에서 현재 정점의 정보만 가지고 있으면 되므로 별도의 자료구조를 사용하지 않고, 재귀함수의 파라미터에 가지고 다녀도 된다. 이 측면에서 BFS보다 코드짜기가 쉬워 BFS와 DFS모두 사용한 문제라면 DFS를 선호하는 편이다.
구현
vector <vector<int>> graph;
bool visit[SIZE];
void dfs(int now){
visit[now] = true;
for(int dst : graph[now]){
if(visit[dst]) continue;
dfs(dst);
}
}BFS에 비해 구현이 비교적 간단하다.
시간복잡도
정점의 개수 V, 간선의 개수 E에 대해 모든 정점과 간선을 한번 씩 방문하므로 O(V+E)로 표현할 수 있다.
추천문제
DFS 기본예제
2667번: 단지번호붙이기
<그림 1>과 같이 정사각형 모양의 지도가 있다. 1은 집이 있는 곳을, 0은 집이 없는 곳을 나타낸다. 철수는 이 지도를 가지고 연결된 집의 모임인 단지를 정의하고, 단지에 번호를 붙이려 한다. 여
www.acmicpc.net
4963번: 섬의 개수
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 지도의 너비 w와 높이 h가 주어진다. w와 h는 50보다 작거나 같은 양의 정수이다. 둘째 줄부터 h개 줄에는 지도
www.acmicpc.net
2644번: 촌수계산
사람들은 1, 2, 3, …, n (1 ≤ n ≤ 100)의 연속된 번호로 각각 표시된다. 입력 파일의 첫째 줄에는 전체 사람의 수 n이 주어지고, 둘째 줄에는 촌수를 계산해야 하는 서로 다른 두 사람의 번호가 주어
www.acmicpc.net
위 예제들은 단순 탐색이기에 BFS와 DFS모두 사용이 가능하다.
응용된 심화버전 문제
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
3109번: 빵집
유명한 제빵사 김원웅은 빵집을 운영하고 있다. 원웅이의 빵집은 글로벌 재정 위기를 피해가지 못했고, 결국 심각한 재정 위기에 빠졌다. 원웅이는 지출을 줄이고자 여기저기 지출을 살펴보던
www.acmicpc.net
DFS는 응용될 수 있는 곳이 상당히 많다. 어느 상황에서든지 응용할 수 있는 능력이 필요하다.
'코딩테스트 준비 > 알고리즘' 카테고리의 다른 글
| 유니온 파인드(Union Find) (0) | 2021.08.26 |
|---|---|
| 위상정렬 (Topological Sort) 알고리즘 (0) | 2021.08.26 |
| 펜윅트리(Fenwick Tree) 자료구조 (0) | 2021.08.26 |
| 세그먼트 트리(Segment Tree) 자료구조 (0) | 2021.08.26 |
| BFS(Breadth-First Search) (0) | 2021.08.26 |





